Over de Sectio Divina en Fibonacci
De Gulden Snede als de natuurlijke verhouding, als symbool van de volkomenheid.
De wiskundige Fibonacci (13de eeuw) onthulde phi via een reeks van getallen die naar hem is genoemd de Fibonacci reeks. De reeks begint met nul en een, en elk volgend getal in de reeks is de som van de twee voorgaande getallen:
0 + 1 = 1; 1 + 1 = 2; 2 + 1 = 3; 3 + 2 = 5; 5+ 3 = 8; 8 + 5 = 13 enz… tot in het oneindige.
Of: de reeks ontstaat als in de opeenvolgende breuken de noemer van de vorige breuk als teller wordt gebruikt, en de som van de vorige teller en noemer:
1 1 2 3 5 8 13
1 2 3 5 8 13 21
Op deze manier vindt de drievuldige natuur van eenheid weer een andere, diepzinnige expressie.
Aldus is de gulden snede een verhouding:
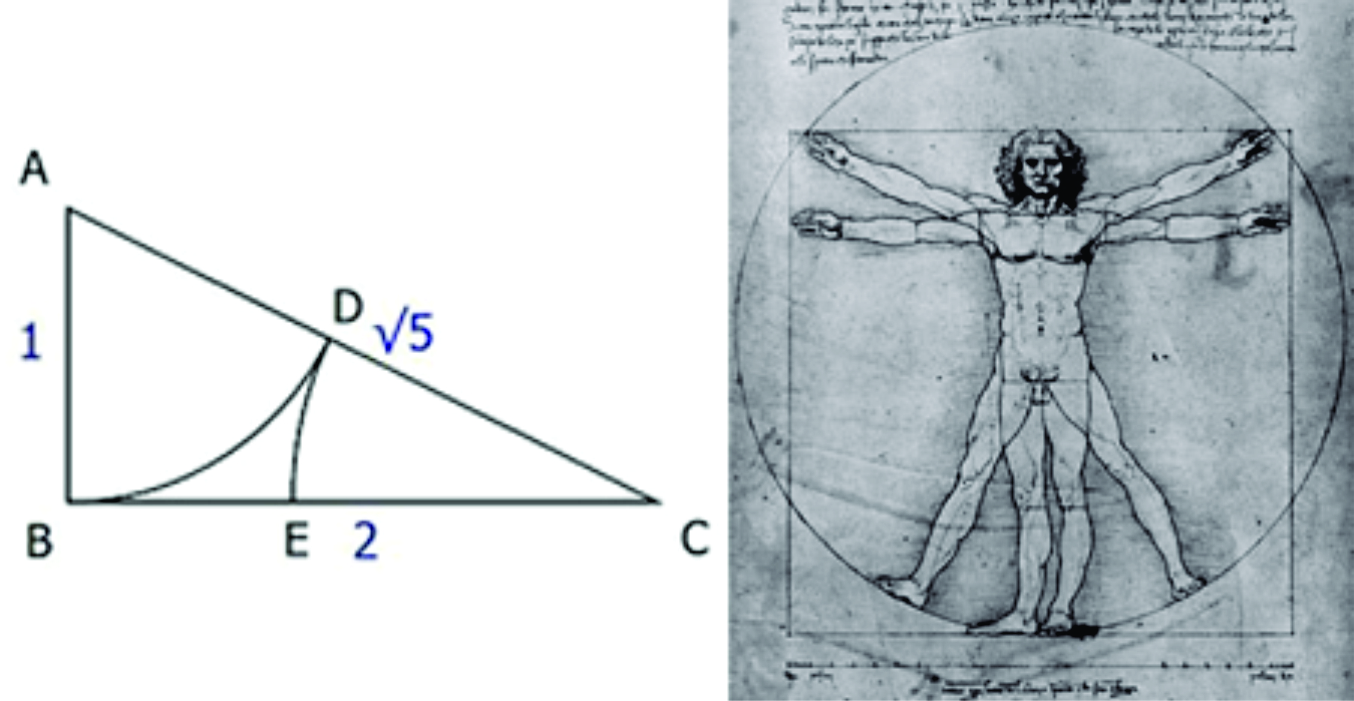
De Fibonacci reeks laat zicht tot in het oneindige verlengen. Door nu iedere term te delen door zijn voorganger, ontstaat er een reeks van verhoudingen: de ratio’s 1 : 1; 2 : 1; 3 : 2;
5 : 3; 8 : 5; 13 : 8; 21 : 13; 34:21; 55 : 34; 89 : 55 enzovoort. Wanneer we deze ratio’s converteren tot hun decimale vormen en die uitzetten in een grafiek, ontstaat er een golf die boven en onder de waarde phi pulseert.
Naarmate de reeks zich voortzet, benaderen de pulsen dit onbereikbaar ideaal steeds meer, zonder het ooit te realiseren.
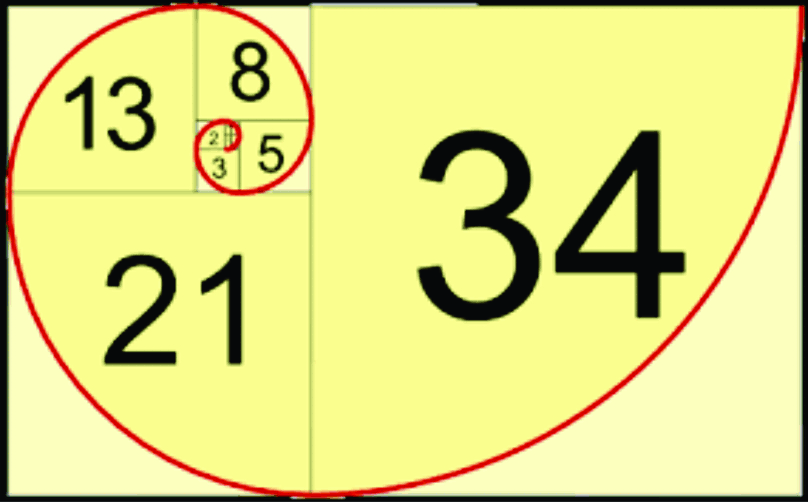
De universele kracht van de Fibonacci reeks kan ook tot expressie worden gebracht als een spiraal, waarin de steeds volmaaktere expressie van phi zichtbaar wordt naarmate het getal zich ontplooit vanuit zijn middelpunt.

Deze zelfreplicatie van phi die we vinden in de evolutie van deze nooit eindigende golven en spiralen is de sleutel tot de alomtegenwoordigheid ervan in natuurlijke vormen. We vinden phi in de manier waarop bladeren zich rond een centrale steel ontvouwen, in het bloemhoofd van een zonnebloem, in de groei van de nautilusschelp, in de vorm van een draaikolk, in de armen van een spiraalnevel(galactisch stelsel) – kortom, overal in de natuur.
